A binary tree is perfect when all levels are complete. In other words, all internal nodes have two child nodes, and the leaves have zero child nodes.
Here is an example of a perfect binary tree:
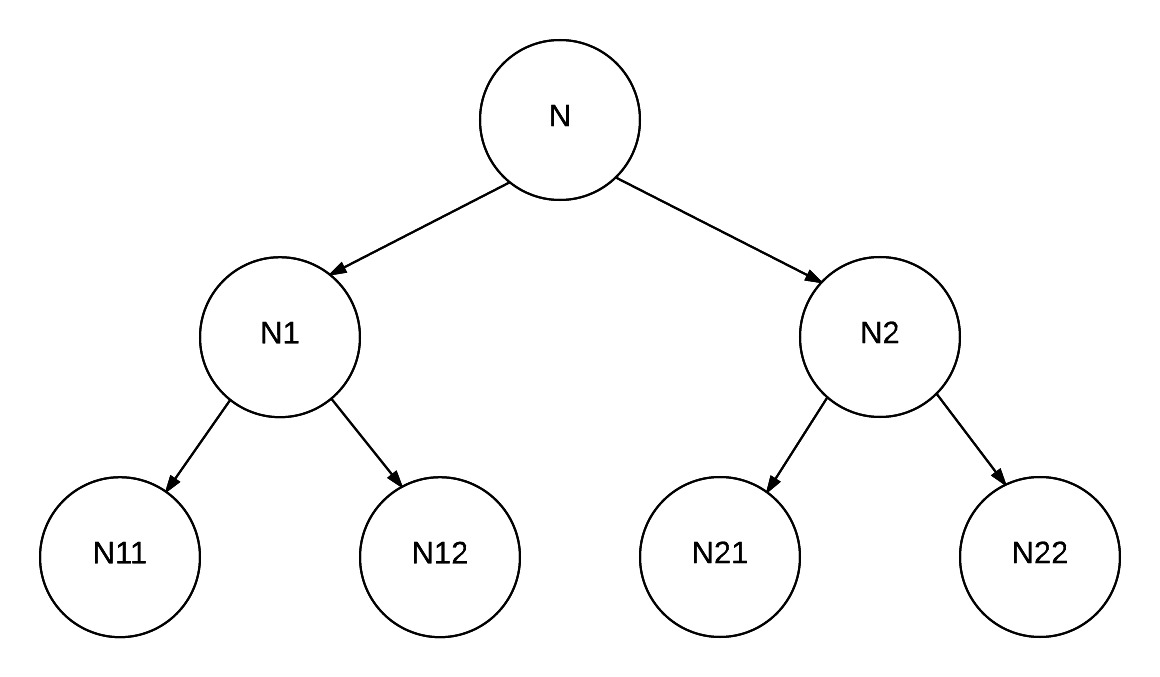
The algorithmic steps to determine if the binary tree is perfect are as follows:
- Find the depth of the tree.
- For all internal nodes, check that both left and right child nodes are present.
- For all leaf nodes, check that no child nodes are present.
First, let’s write a Java method to calculate the tree depth. In a perfect binary tree, all leaves have the same depth. Therefore, we can calculate the depth of the leftmost leaf:
private int depth(TreeNode node) {
return node.left() != null ? 1 + depth(node.left()) : 1;
}
Then, we need a method to check if the tree is perfect, given the depth of the current node and the tree depth:
private Boolean isPerfectTree(TreeNode node, int depth, int treeDepth) {
// check for the leaf nodes
if (depth == treeDepth && (node.left() == null && node.right() == null)) {
return true;
}
// check for internal nodes (depth != treeDepth)
if ((node.left() != null && node.right() != null)) {
return isPerfectTree(node.left(), 1 + depth, treeDepth) &&
isPerfectTree(node.right(), 1 + depth, treeDepth);
}
return false;
}
Putting it all together we have:
public Boolean isPerfectTree(TreeNode node) {
int treeDepth = depth(node);
return isPerfectTree(node, 1, treeDepth);
}
private int depth(TreeNode node) {
return node.left() != null ? 1 + depth(node.left()) : 1;
}
private Boolean isPerfectTree(TreeNode node, int depth, int treeDepth) {
// check for last level node
if (depth == treeDepth && (node.left() == null && node.right() == null)) {
return true;
}
// check for inner levels
if ((node.left() != null && node.right() != null)) {
return isPerfectTree(node.left(), 1 + depth, treeDepth) &&
isPerfectTree(node.right(), 1 + depth, treeDepth);
}
return false;
}
You can practice the perfect tree check exercise here.